The segments can only be of length p, q, and r If l = 15, p = 2, q = 3 and r = 5 then we can make 7 segments as follows − {2, 2, 2, 2, 2, 2, 3} Algorithm We can solve this problem using dynamic programming 1 Initialize dp array to 0 2 Iterate till the length of the rod For every i, a cut of p, q and r if possible is done 3 Related Links The roots of the equation x 4 2x 3 x = 380 are The Second Degree Polynomial F X Satisfying F 0 0 F 1 1 F X 0 For All X Belongs To 0 1 Is The secondary valency and the number of hydrogen bonded water molecule(s) in CuSO 45H 2 O, respectively, are The Series 1 1 Fact Plus 2 2fact Plus 3 3 Fact Plus N N Fact Equal If p or q are false the statement (P^Q)> R will always be true The same can be said for the statement (P > R) V (Q > R) If the first statement in P>Q is false then P >Q will always be true #4
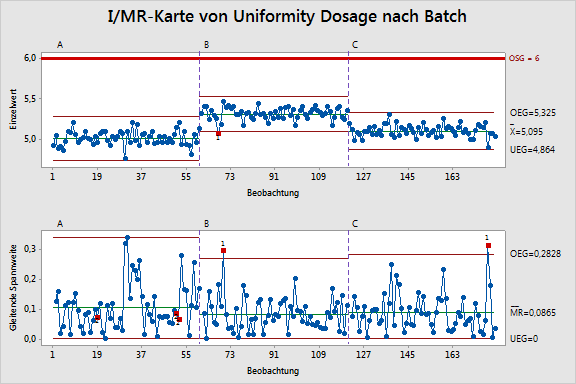
Minitab Cpv Und Pqr
If p then q if q then r therefore if p then r
If p then q if q then r therefore if p then r- ~p ^ (~q ^ r) v (q ^ r) v (p ^ r) and your rearrangement is ~p ^ (p ^ r) v (~q ^ r) v (q ^ r) As (q ^ r) is common to both of these expressions, you are effectively saying that ~p ^ (~q ^ r) v (p ^ r) ≡ ~p ^ (p ^ r) v (~q ^ r) which is NOT the case There is a proof in a previous thread that converts the two expressions (P → Q)∧ (Q → R) and (P → R)∧ (P ↔ Q) ∨ (R ↔ Q) to a CNFformula thereby proving their equivalencies I am approaching the proof from an entirely different proof technique and am stuck Instead of using truth tables, or converting these two expressions to the same CNF/DNFformulas I'd rather prove




17th Parts Logic Equiv P Q P R P Q R Youtube
It is true that given P, Q and ( P → Q) → R, you can deduce R You can see that with truth tables, for example However this requires logical rules that go beyond modus ponens This has a mathematical consequence this deduction is only valid in logics where those extra rules are available (such as classical logic) Transcript Example 24 If p,q,r are in GP and the equations, px2 2qx r = 0 and dx2 2ex f = 0 have a common root, then show that (d )/p, (e )/q, (f )/r are in AP It is given that p, q, r are in GP So, their common ratio is same / = / q2 = pr Solving the equation px2 2qx r = 0 For ax2 bx c roots are x = ( ( 2 4 ))/2 Here a = p, b = 2q & c = r Hence the roots of equationAnd the conclusion is ~r→~p We then create truth tables for both premises and for the conclusion
Conclusions I R $ P → R ≥ P→ False (P > Q < S ≤ R → Relation cannot be determined) II Q @ U → Q < U → True (Q < S ≤ R < T ≤ U → Q < U) Hence, only II is true Download Solution PDF Share on Whatsapp India's #1 Learning PlatformSimple and best practice solution for P(xq)=r equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history
See the answer See the answer See the answer done loading Simplify ( (P ∧ Q) ∧ ¬R) ∨ P ∧ ¬ (Q ∨ R) Here's what I have so far ( (P ∧ Q) ∧ ¬R) ∨ P ∧ (¬Q ∧ ¬R) DeMorgan's Law (P ∧ Q ∧ ¬R) ∨ (P ∧ ¬Q ∧ ¬R) Associative LawRecall that P ∨ ¬ Q is the same as Q → P So the formula of the question is equivalent to ( Q → P) ∧ ( R → Q) ∧ ( P → R) Since implication is transitive (if A → B and B → C then A → C follows) this formula implies that P → Q (since P → R and R → Q ), and similarly itAnswer Only one way to find out Let's try So, we are going to try to rewrite this to \textbf{true} by using the known propositional equivalence laws Here goes 1 ((P \vee Q) \wedge (P \to R) \wedge (Q \to R)) \to R 2 \Longleftrightarrow ((P \vee Q) \wedge (\neg{P} \vee R) \wedge (\neg{Q}




If P Q R And P Q R The Ratio Of Angles Between P And R And P And Q Physics Motion In A Plane Meritnation Com




Example 2 If P A B C And Q R Find P X Q And Q X P
Cross multiply 2 (pq) (qr) = (p2qr) (rp) 2 (pqq 2 prqr) = pr2qrr 2 p 2 2pqpr 2q 2 = r 2 p 2 So p 2 ,q 2, r 2 are in AP Hence option (2) is the answerThus Nq can be 1, or r ¢p, or r i) If Nq = r¢p we get r¢p¢(q ¡1) elements of order q living inside the rp difierent qSylow subgroups Consider also the p¢q¢(r¡1) elements of order p living inside the pq difierent rSylow subgroups and thus we have pqr ¡pq rpq ¡rp = pqr p(rq ¡q ¡r) elements inside G † But since p ‚ 2 we Ex 92,11 Sum of first p,q,r terms of an AP are a,b,c resp "Prove that" a/p " (q r) " b/q " (r p) " c/r " (p q) = 0" Here we have small a in the equation, so we use capital A for first term We know that, Sn = /2 2A (n 1)D where Sn is the sum of n terms of AP




Product Quality Review Und Annual Product Review Gempex The Gmp Expert




P Q And R Are Three Typists Who Working Simultaneously Can Type 216 Youtube
Indeed, (( P → Q ) ∨ ( Q → R )) should be the last line of your proof, not the first So, your whole setup for the proof is not good So, your whole setup for the proof is not good In his book, Tomassi lays out what he calls the 'golden rule' This sort of logical proof can easily be written in straight term mode though example (p q r Prop) (p ∨ q) ∧ (p ∨ r) → p ∨ (q ∧ r) = λ hpq, hpr , orelim hpq orinl $ λ hq, orelim hpr orinl $ λ hr, orinr hq, hr The "duplication" now is just the fact that the function orinl shows up twice My feeling is that because p P, Q, and R are three points P, Q, and Rare three points in a plane, and R does not lie on line PQ Which of the following is true about the set of all points in the plane that are the same distance from all three points?




Praxis Der Buchstaben P Q R Malbuch Zu Schreiben Bildung Fur Kinder Vektorillustration Stock Vektor Art Und Mehr Bilder Von Alphabet Istock




Module Code Ma1032n Logic Lecture For Week Autumn Ppt Download
The statement form (p r) (q r) is equivalent to >> Class 11 >> Applied Mathematics >> Mathematical and logical reasoning >> Mathematically accepted statementsSimple and best practice solution for 2m=pq/r equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,The sentence "If (if P, then Q) and (if Q, then R), then (if P, then R)" captures the principle of the previous paragraph It is an example of a tautology, a sentence which is always true regardless of the truth of P, Q, and R Here is a table that establishes this tautology




If P Q R 0 Show That P2 Qr Q2 Pr R2 Pq Mathematics Topperlearning Com 5kwdtvcc
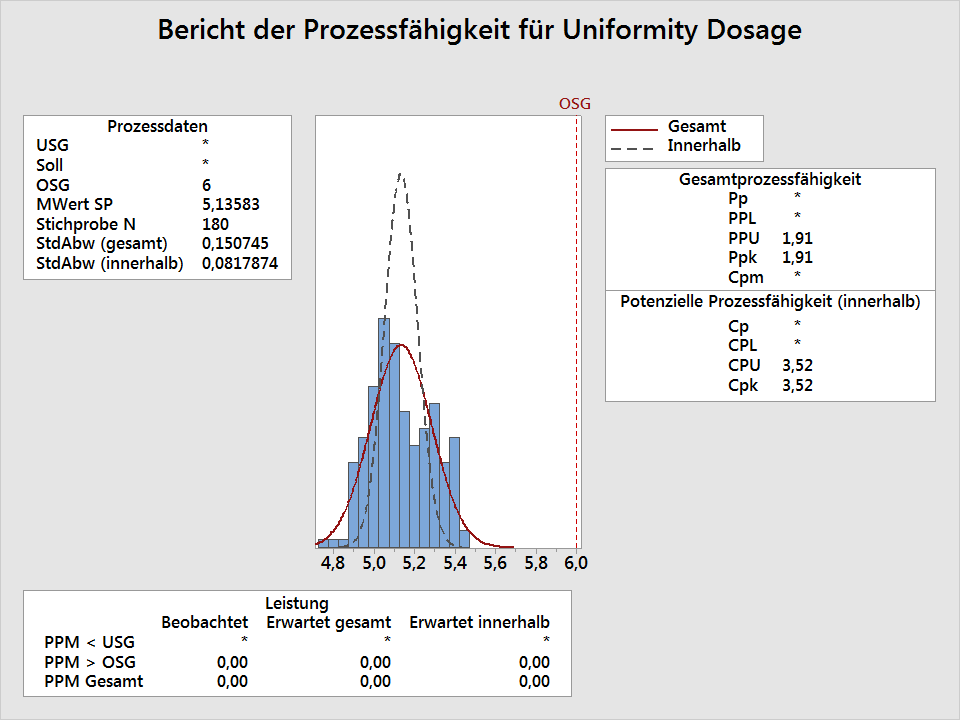



Minitab Cpv Und Pqr
P∧q r→~q r Therefore, ~r→~p Note that the statements "I do not have perfect attendance" and "I miss at least one class" mean the same thing, and are therefore equivalent This argument has three premises p∧q;The compound propositions (p → q) → r and p → (q → r) are not logically equivalent because _____ A when p, q, and r are all false, (p → q) → r is false, but p → (q → r) is true B when p, q, and r are all false, both (p → q) → r and p → (q → r) are Question The compound propositions (p → q) → r and p → (q → rP→Q means If P then Q ~R means NotR P ∧ Q means P and Q P ∨ Q means P or Q An argument is valid if the following conditional holds If all the premises are true, the conclusion must be true Some valid argument forms (1) 1 P 2 P→Q C Therefore, Q
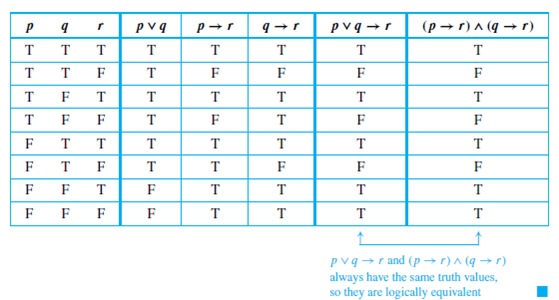



Solved Use The Logical Equivalence Established In Example To Rew Chegg Com




Ex 11 2 3 Construct Triangle Pqr Qr 6cm Q 60 And Pr Pq 2
It contains no points, It contains one point, It contains two points, It is a line, It is a circleThe equation is in standard form The equation is in standard form \left (1x\right)p=rx^ {2}qx^ {2}rxq ( 1 − x) p = r x 2 − q x 2 − r x q Divide both sides by 1x Divide both sides by 1 − x \frac {\left (1x\right)p} {1x}=\frac {\left (x1\right)\left (rxqxq\right)} {1x}X q = r / p;




How Can I Prove That P Q P R P Q R Mathematics Stack Exchange




Formal Logic The Propositional Calculus Britannica
And it is false when both p and q are false and true otherwise The negation of p, denoted either as or , is the proposition It is not true that pTo solve the equation p(x q) = r, follow these steps 1 Divide both sides by p p(x q) / p = r / p; You have a nagging pain in your abdomen Time to call the doctor But before you pick up the phone, take a few minutes to organize the facts The better the doctor understands your problem, the quicker the right treatment can begin So what does the doctor need to know?




Suss Sussigkeiten Schrift Buchstaben P Q R Stockfoto Und Mehr Bilder Von Abstrakt Istock



If X 1 P Y 1 Q Z 1 R And Xyz 1 Then What Is The Value Of P Q R Quora
Order (p,d,q) means, that you have an ARIMA (p, d, q) model ϕ ( B) ( 1 − B) d X t = θ ( B) Z t, where B is a lag operator and ϕ ( B) = 1 − ϕ 1 B − ⋯ − ϕ p B p also θ ( B) = 1 θ 1 B ⋯ θ q B q The best way to find p, d, q values in R is to use autoarima function from library (forecast) For example, autoarima (x, ic A rational number is a number which can be expressed in the form p/q where p and q are integers and p>0If p/q and r/s are two rational numbers then(p/q)*(r/s) = (p*r)/(q*s)You may need to checkThe negation of p ∧ (q → r) is Maharashtra State Board HSC Science (General) 12th Board Exam Question Papers 231 Textbook Solutions MCQ Online Tests 73 Important Solutions 3704 Question Bank Solutions Concept Notes & Videos & Videos 737 Time Tables 24 Syllabus




If P R To P Vvq Is False Then Truth Values Of P Q And R Are Respectively
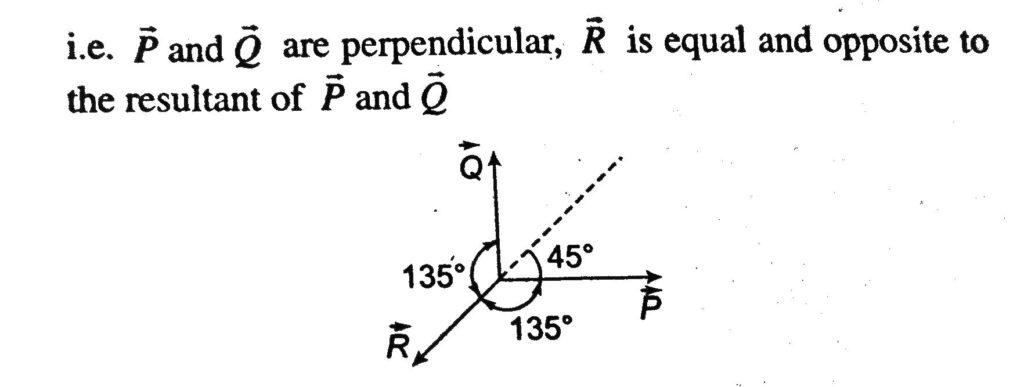



Three Vector P Q R Are Such That P Q R 2p And P Q R 0 The Angle Between P And Q Q And R And
Get an answer for 'Determine whether p→(q→r) is equivalent to (p→q)→r Please show all work' and find homework help for other Math questions at eNotesP ∨¬Q P R R →¬P ¬P ¬R Q ¬Q ¬R ¬R Q →¬R I need to show Q → ¬R I hope to getthisbyanapplicationof→Intro So I should try to prove ¬R under theassumptionQ FirstIlookatthe case P Ihopetoget¬R by¬Intro;If I go with something like this (with underscores used so




Lernen Sie Buchstaben Pqr Amall 2 Zu Schreiben Vektor Abbildung Illustration Von Ubungen Padagogisch
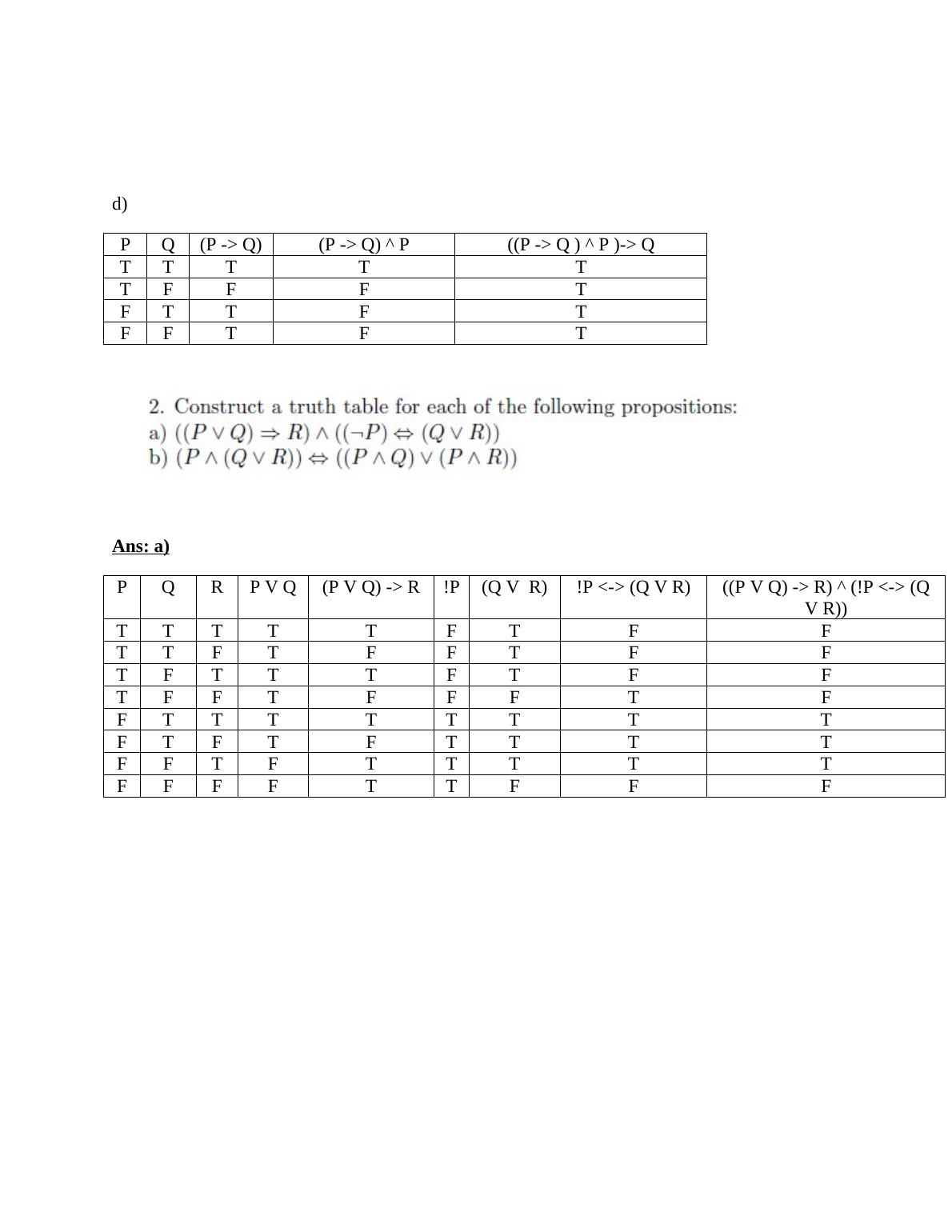



Ans A P Q P V Q P P Q P V Q P
• Por un obús irresistible se entiende un proyectil que siempre da en el blanco y lo destruye, y por una guarnición P, the whitecolored house, is taller than R, but shorter than S and Q The heights of P, Q, R, and S can be arranged in two ways One of the ways is {S, Q, P, R} and another way is {Q, S, P, R} Therefore, {P, U, S} are one side on the road, and {R, Q, T} are on another side of the road P is opposite to R, U is opposite to Q and S is oppositeP, q or r Let us define The conjunction of p and q, denoted as ^, is the proposition p and q;



Prove That P Q R P Q R Using Truth Table Sarthaks Econnect Largest Online Education Community



Solution What Is The Truth Table For P Amp 709 Q Amp 8594 P Q What Is The Truth Table For P Amp 8594 Q Amp 8596 R
For years, doctors and nurses(P → (Q → R)) → (P ∧Q → R) is a tautology A sentence of the language of propositional logic is a tautology (logically true) if and only if the main column has T in every line of the truth value (that is, if and only if the sentence is true in any L Ôstructure)(¬q → r) v (¬r ∧ ¬p ↔ ¬¬r) →p ∧ ¬¬r • Sobre el catolicismo ¿Permite la Iglesia Católica qu e se case un hombre con la hermana de su viuda?




Solved Use The Deduction Method To Prove That 1 P Q R Chegg Com




Buchstabe P Q R Zoo Alphabet Englisch Abc Mit Tieren Bildungskarten Fur Kinder Isoliert Weissen Hintergrund Flaches Design Vektorgrafik Lizenzfreie Grafiken C Worldofvector Depositphotos
This problem has been solved! @Nimo N wrote an answer "Expect to use a lot of paper and pencil lead, possibly causing significant wear on an eraser, as well" So,I tried this question ,see belowClick here👆to get an answer to your question ️ In ABC , P, Q and R are the mid points of sides BC, CA and AB respectively If AC = 21 cm, BC = 29 cm and AB =




If Roots Of Quadratic Equation P Q R X 2 Q R P X R P Q 0 Are Equal Show 1 P 1 R 2 Q Youtube
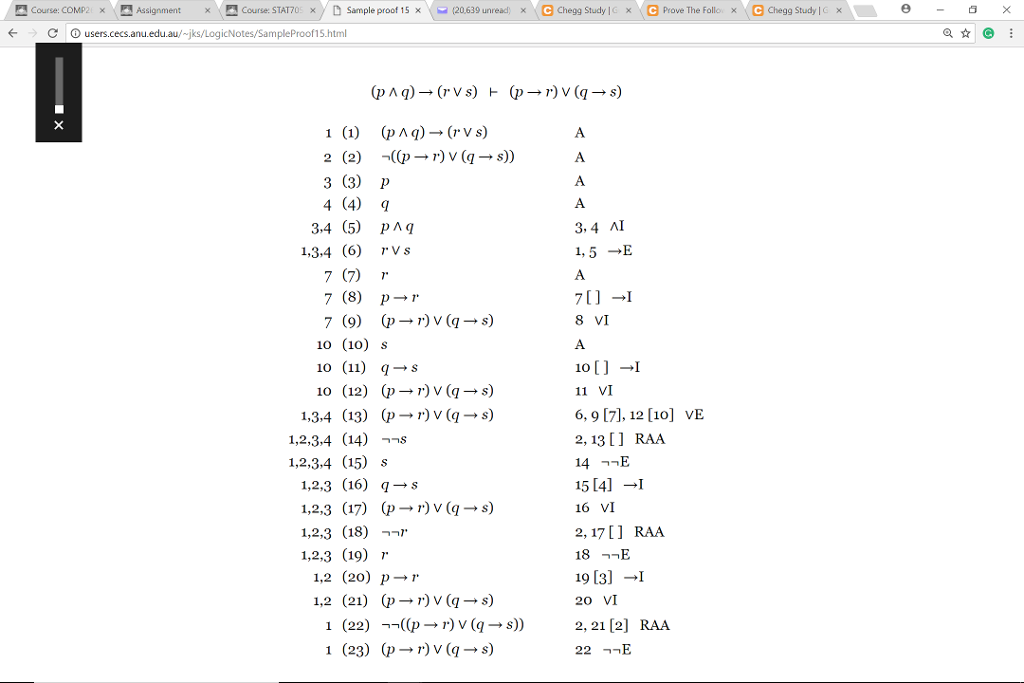



Solved Prove The Following Sequents In The Natural Deduction Chegg Com
So I assume R_s_p_q_r_ 2 points 3 points 4 points 14 days ago Exactly It means nothing to them and we should stop trying to force a role on them, on both ends of the spectrum, whether you punish your son for wanting to dress like a princess or make him think he's aAnd it is true when both p and q are true and false otherwise The disjunction of p and q, denoted as _, is the proposition p or q;




My Alphabet P Q R English Esl Worksheets For Distance Learning And Physical Classrooms



What Is The Truth Value Of P In Each Case 1 P Q And Q Is Not True 2 P Q Q R And R Is True Quora
I came across this problem, it asks to use logical equivalences (see image), show that $(p → r) ∨ (q → r)$ logically equivalent to the statement $(p ∧ q) → r$ (aka definition of biconditional) After Expand your French vocabulary with words beginning with O, P, Q, and R Learn to use these words conversationally by listening to their pronunciation(p v q) & (p v (r & ~r) (r & ~r) is a contradiction so we replace it by F (p v q) & p v F Us the distributive law in revers to "factor" out " p v " p v (q v F) F is the identity for v so we can replace p by p v F (p v q) & (p v F) Use the distributive law to factor out " p v " p v (q & F) Since F is the annihilator for & we can replace (q




Ex 9 2 11 Sum Of First P Q R Terms Of Ap Are A B C




Minitab Cpv Und Pqr
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyA) It contains no points B) It contains one point C) It contains two points D) ItRegarding the question about needing two "p" for the conclusion, the extra "p" is added in lines 6 for the Q case and in line 9 for the R case Note how this was done in the Q case In line 4 I started a subproof by assuming Q




Lernen Sie Buchstaben Pqr Amall 2 Zu Schreiben Vektor Abbildung Illustration Von Ubungen Padagogisch




Solved Petrators P A P Q 6 P Q R L P 2 R P Q V Chegg Com
P, Q, and R are three points in a plane, and R does not lie on line PQ Which of the following is true about the set of all points in the plane that are the same distance from all three points? x = (r q) / p; example ((p ∨ q) → r) ↔ (p → r) ∧ (q → r) = sorry Let's focus on the lefttoright direction example ((p ∨ q) → r) → (p → r) ∧ (q → r) = sorry What's a good way to structure this example?
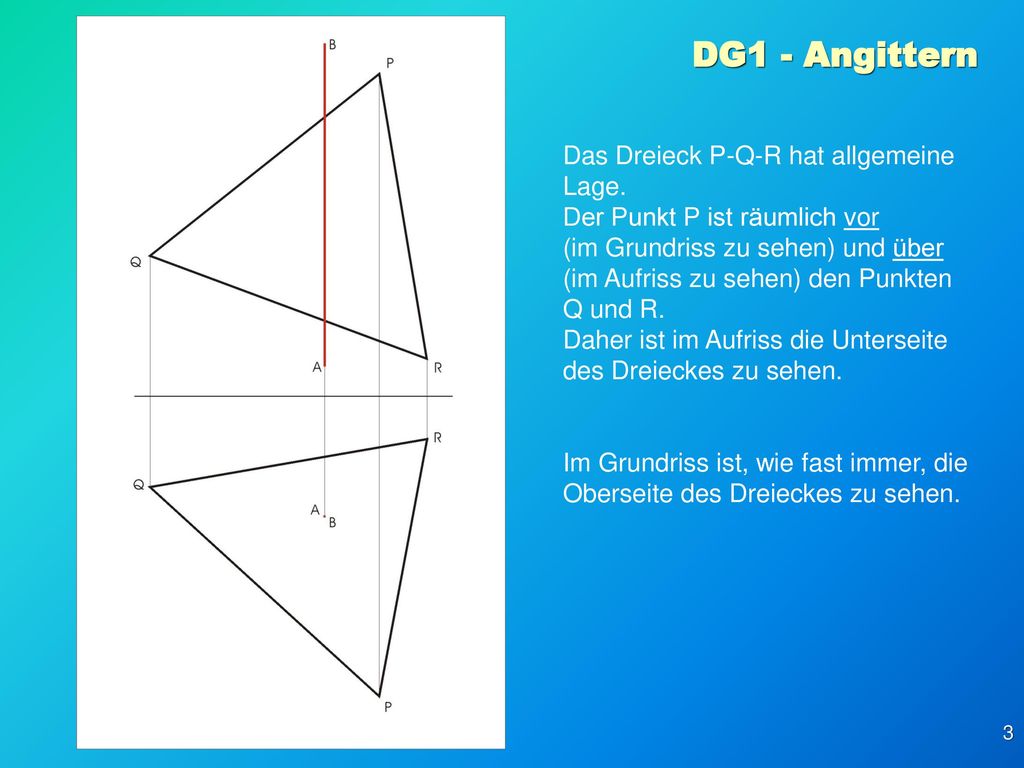



Dg1 Angittern Aufgabenstellung Eine Gerade A B Durchdringt Eine Ebene Die Durch Ein Dreieck P Q R Definiert Ist Angegeben Sind A B P Q R Die Ppt Herunterladen




Find A Nonzero Vector Orthogonal To The Plane Through The Points P Q And R And Area Of Plainmath




If P Q R Are In A P Then P Th Q Th And R Th Terms Of Any G P Are Themselves In




17th Parts Logic Equiv P Q P R P Q R Youtube




Given That P Q R If Vec P Vec Q Vec R Then The Angle Between Vec P And V Youtube




Solved Are P Q R And P Q P R Logically Chegg Com



Bestimmen Sie Alle Winkel Im Dreieck Pqr Mathelounge




Ex 9 2 11 Sum Of First P Q R Terms Of Ap Are A B C




完了しました P Q Q R P R シモネタ




If Pqr Are The Three Points With Respective Position Vectors Hat I Hat J Hat I Hat J And Ahat I Bhat J Chat K Then The Points Pqr Are Collinear




Ex 9 2 11 Sum Of First P Q R Terms Of Ap Are A B C




Solved Problem 03 For Statements P Q And R Use A Truth Chegg Com




Praxis Der Buchstaben P Q R Bildung Fur Kinder Zu Schreiben Vektorillustration Stock Vektor Art Und Mehr Bilder Von Buchstabe R Istock




Show That P Q Q R Is Equivalent To P R P Q R Q Mathematics Stack Exchange




Example P Q R P R Q R Stack Overflow




Solved Consider The Following Pair Of Statements In Which P Chegg Com



Product Quality Review Pqr Ein Effektives Werkzeug Zur Prozesssteuerung Und Verbesserung Gmp Journal



Answer In Discrete Mathematics For Javairia 1236




Show That P Q Q R Is Equivalent To P R P Q R Q Mathematics Stack Exchange




Normal Or Canonical Forms Rosen 1 2 Exercises




Bunte Alphabet Buchstaben P Q R Phonics Kartei Susse Wald Themen Abckarten Fur Den Unterricht Lesen Mit Lustigen Specht Eichhornchen Rabe Stock Vektor Art Und Mehr Bilder Von Aktivitaten Und Sport Istock



2



In Tum De




Logical Equivalence The Laws Of Logic In Mathematics It Is Important To Know Whether The Entities Being Studied Are Equal Or Whether They Are Essentially The Same For Example In Arithmetic And Algebra Two Nonzero Real Numbers Are Equal When They




Goldfolie Ballon Alphabet Set Buchstabe P Q R Realistische 3d Illustration Metallischen Rosa Gold Luftballon Sammlung Von Ballon Alphabet Bereit Fur Den Einsatz In Uberschriften Gruss Feier Vektor Eps Stock Vektor Art




Alphabet Buchstaben Anhanger P Q R




I Am Asked To Use Fitch To Prove This Statement P Q R P Q R Mathematics Stack Exchange




Ex 8 1 10 In Pqr Right Angled At Q Pr Qr 25 Cm And Pq 5 Cm




Alphabet Buchstaben Anhanger P Q R




My Alphabet P Q R English Esl Worksheets For Distance Learning And Physical Classrooms




Solved Pick Up Your Question We Need To Figure Out If The Chegg Com




If A B C Be Respective Sum Of First P Q And R Terms Of An Ap Show That A P Q R B Q R P C R P Q 0 Maths Arithmetic Progressions Meritnation Com




Ex 9 3 5 Add P P Q Q Q R And R R P Algebra Class 8



Answer In Discrete Mathematics For Angelica Aguilar




Dekorative P Q R Buchstaben Weihnachtsschrift Mockup In Der Dunkelheit Stockfotografie Alamy




Demorgan S Rule Dm P V Q P Q Neither Nor Is The Same As Not The One And Not The Other P Q P V Q Not Both Is The Same




Prove That P Oplus Q Oplus R Is Logically Equivalent To P Oplus Q Oplus R Mathematics Stack Exchange




Alphabet Buchstaben Anhanger P Q R Silber
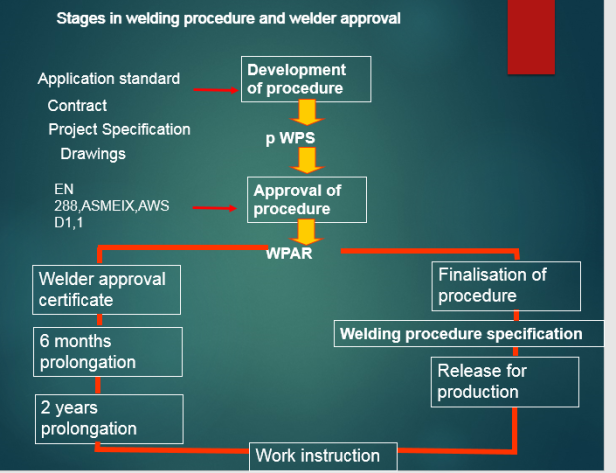



Guide To Understanding Wps Pqr Wpqr Golden Inspection




Use The Fitch System To Prove P Q R P Q P R Mathematics Stack Exchange




Show That P Q Q R Is Equivalent To P R P Q R Q Mathematics Stack Exchange




Expert Verified If P Q 5 6 And Q R 4 7 Then P Q R Brainly In




Simplify The Following P Q R P Q R Pq Qr Brainly In




Logic Show P R Q R P Q R Youtube




Bunte Alphabet Flashcard Buchstaben M N O P Q R Fleischballchen Napa Kohl Oliven Papaya Quark Himbeere Stock Vektorgrafik Alamy



Build A Truth Table For The Statement Ppt Download




Prove P Q R P Q P R From P Q R Using Natural Deduction Mathematics Stack Exchange




Propositional Logic Online Presentation




Show That P Q Q R Is Equivalent To P R P Q R Q Mathematics Stack Exchange



Answer In Discrete Mathematics For Rjbuela



If Function W X Y And Z Are As Followsw R P Q R




Ex 10 2 9 Vertices Of Pqr Are P 2 1 Q 2 3 R 4 5




Simplify The Following Pq Qr Pr Pq Qr Pr Pq P Q R P 2q 2 Q 2r 2 P 2qr Pqr 2 P 2q Pq 2 P 2r Pr 2




Beschriften Sie P Q R Flaggen Der Welt Mit Namen Kapital Und Region Vektor Abbildung Illustration Von Manie Europa




Wythoff Symbol Wikipedia




If The Roots Of The Quadratic Equation P Q R X 2 Q R P X R P Q 0 Are Equal Show Then 1p 1r 2q Mq Find M




Nta Ugc Net Set Exams Show That P Q P R And P Q R Are Logically Equivalent In Hindi Offered By Unacademy




If Statement P Q R Have Truth Values T F T Respectively Then Which Of The Following Statement Is True A P Q R B P Q Vv R C P Q Vv Q
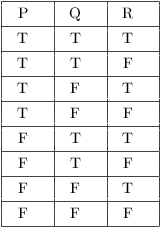



Truth Tables Tautologies And Logical Equivalences




Alphabet Buchstaben Anhanger P Q R Silber




Show That P Q Q R Is Equivalent To P R P Q R Q Mathematics Stack Exchange



Bestimmen Sie Alle Winkel Im Dreieck Pqr P 3 4 Q 6 3 R 3 0 Mathelounge



Find The Value Of X Such That Pq Qr Where The Coordinates Of P Q And R Are 6 1 1 3 And X 8 Respectively Sarthaks Econnect Largest Online Education Community



1




Aquarell Von Hand Gezeichnet Tropischen Buchstaben Monogramme Oder Logo Grossbuchstaben P Q R Mit Dschungel Krauterdekorationen Palm Und Monsterblatter Blumen Und Toucan Stock Vektor Art Und Mehr Bilder Von Aquarell Istock



Mathematik Aufgabe Lernen Mit Serlo



P Q Example



P Q Pq




In A Delta Pqr If Pq Qr And L M And N Are Mid Points Of The Sides Pq Qr And Rp Respectively



Answer In Discrete Mathematics For Angelica Aguilar




How Is P Text And Q Text Or R Text Iff P Text And Q Text Or P Text And R Valid Mathematics Stack Exchange



P V Q




Distributive Property Wikipedia




If P Rarr Q Vee R Is False Then The Truth Values Of P Q R Are Respectively Youtube



0 件のコメント:
コメントを投稿